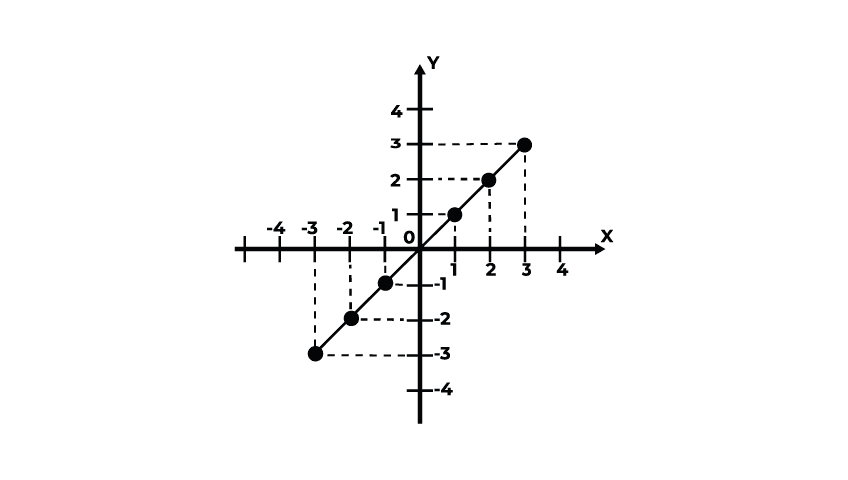
A função afim, também conhecida como “função do primeiro grau”, é aquela na qual o maior expoente da incógnita (parte literal) é 1. A função afim possui características particulares, que a definem, como sua raiz, coeficientes linear e angular e sua representação por meio de uma reta no plano cartesiano (como na imagem deste post). A função afim é representada por f(x)=ax+ b.
- Raiz - valor da incógnita (x) quando y=0, tal que o número máximo de raízes de uma função está diretamente ligado ao grau da função (maior expoente da incógnita). Assim, a função afim irá sempre possuir somente uma raiz. Para encontrar a raiz, pela definição, teremos que resolver a seguinte equação: ax+b=0. Assim, x=-b/a. Por isso, a raiz de uma função do primeiro grau será sempre um ponto R(-b/a,0) que define o local em que a reta (função afim) corta o eixo Ox (eixo das abscissas);
⠀
- Coeficiente linear - o coeficiente linear da função afim é o termo independente “b” da função e este determina o ponto P em que a função (reta) corta o eixo Oy (eixo das ordenadas). P é dado por P(0,b);
⠀
- Coeficiente angular - o coeficiente angular da função afim, também chamado de taxa de variação, por fornecer a que taxa y varia em relação a x, será sempre igual ao coeficiente “a” que multiplica a incógnita x. Para calcular o coeficiente angular precisamos de 2 pontos, depois basta calcular a variação das coordenadas em y entre os dois pontos dividida pela variação das coordenadas em x.
Diversas grandezas em nosso dia-a-dia se relacionam de forma que podemos representar por meio de uma função afim. Os vendedores de algumas lojas por exemplo, eles ganham o salário fixo mensal mais uma gratificação em cima da quantidade de produtos vendidos (x). Veja abaixo como isso pode ser representado.
⠀
Ganho = Salário Fixo + Gratificação . x
Você gostou dessa dica de matemática? Deixe aqui seu comentário👇

Deixe um comentário