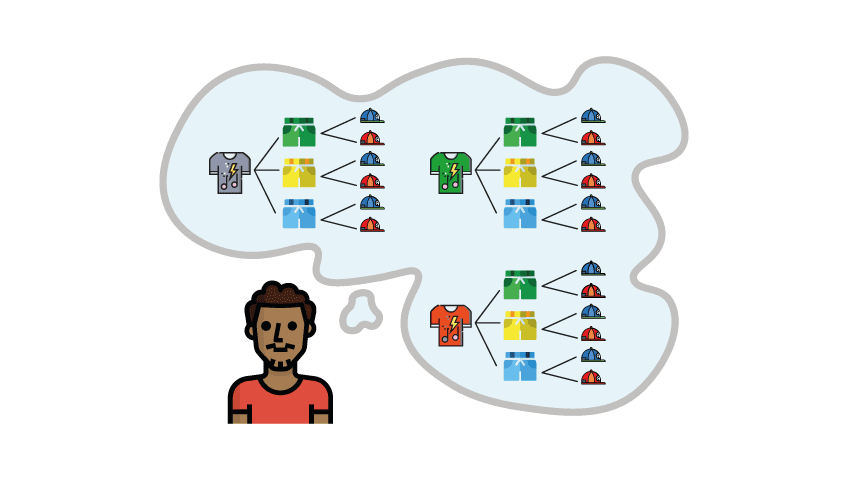
Análise combinatória é uma área da matemática que estuda a resolução dos problemas que envolvem contagem, utilizada principalmente em problemas de estatística e probabilidade. Utilizando o princípio fundamental da contagem, temos que, para saber o número total de opções dentro de um determinado evento, devemos multiplicar as opções apresentadas. Veja um exemplo: Adrian possui 3 camisetas, 2 bonés e 3 bermudas. De quantas formas distintas ele poderá se vestir?
Observe que para tal problema, para cada camiseta, teremos 2 possibilidades de bonés e para cada boné e camiseta, teremos 2 possibilidades de bermudas. Dessa forma, Adrian terá 3.3.2 possibilidades de se vestir, o que resulta em 3.3.2=18 possibilidades.
Utilizamos bastante o conceito de fatorial, que é a operação dada pelos produtos dos números positivos inteiros de um número natural "n"; Por exemplo: o fatorial do número 5 é escrito como 5! e operamos como, 5.4.3.2.1=120.
Na combinatória temos basicamente, 3 tipos distintos de operações. Nas descrições abaixo "n" e "k" são as possibilidades dentro de um evento.
Permutação - qualquer sequência reordenada proveniente de uma sequência ordenada, de modo que se um conjunto X é uma permutação de Y, então ambos possuem os mesmos elementos, ordenados de maneiras distintas. A simples é expressa por: Pₙ=n!;
Arranjo - são formas de agrupamentos de elementos nas quais a ordem dos elementos é levada em consideração. No arranjo simples não existirá repetição de elementos no agrupamento. Pode ser expresso como: Aₙ,ₖ=n!/(n-k)!
Combinação - é como o arranjo, diferenciando-se somente pela ordem que gera um resultado ser indiferente, ou seja, a ordem não irá importar. Pode ser expresso como: Cₙ,ₖ=n!/k!(n-k)!
Você gostou dessa dica de matemática? Deixe aqui seu comentário👇

Deixe um comentário