Nós estamos acostumados a estudar as parábolas quando aplicamos conceitos das funções quadráticas, afinal, elas são usadas para representar geometricamente essas funções. Na geometria analítica, nós estudamos os elementos que constituem as parábolas dentro do estudo das cônicas, que englobam, entre outras figuras, os cones e hipérboles, por exemplo.
As figuras deste post ilustram as quatro situações que podemos encontrar ao estudarmos a parábola. Os elementos apresentados na imagem são:
- Foco (F) - é o ponto usado para a definição da parábola, a partir dele a parábola é formada;
- Reta diretriz (d) - é a uma reta que também usamos na definição da parábola. A distância entre um ponto qualquer da parábola e a reta diretriz, tem a mesma distância que esse ponto e o seu foco;
- Parâmetro (P) - o parâmetro é a distância entre o foco e a reta diretriz;
- Vértice (V) - é o ponto da parábola que fica mais próximo de sua reta diretriz. Sua distância até o foco da parábola é igual à metade do parâmetro, assim como a distância entre esse ponto e a reta diretriz também é igual à metade do parâmetro;
- Eixo de simetria (e) – divide a parábola ao meio em partes iguais.
A equação reduzida é útil nessas situações em que o vértice da parábola está centrado na origem do plano cartesiano, caso contrário, é necessário acrescentar termos em cada uma das equações apresentadas. Por exemplo, na primeira equação temos:
X² = 2 . P . y
Se a parábola não estiver com seu vértice na origem, temos:
(X - X₀)² = 2 . P . (y - y₀)
Onde “X0” e “Y0” diz respeito as coordenadas do vértice. Isso é feito para as outras equações.

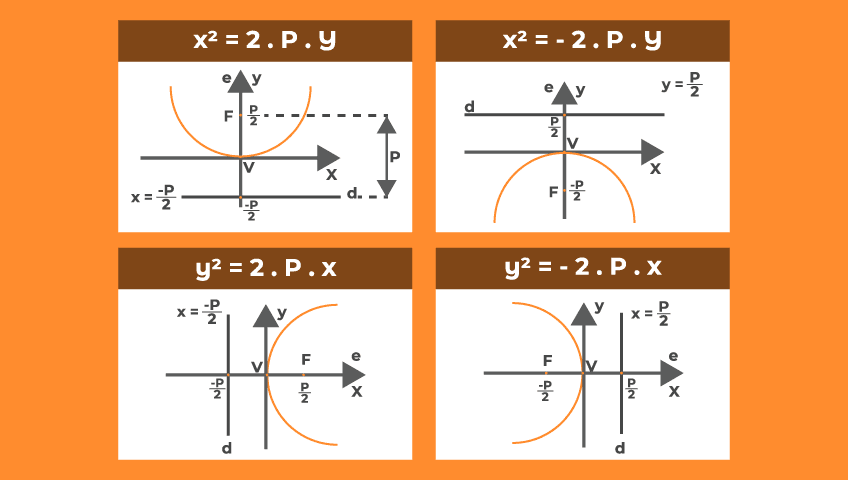
Deixe um comentário