Geometria da elipse

A elipse é uma das cônicas estudadas na geometria analítica. Ela descreve o movimento dos planetas ao redor do Sol, por exemplo. Matematicamente, ela é definida como o conjunto de pontos cuja soma da distância entre esses pontos com a distância entre cada um de seus focos é sempre constante.

 

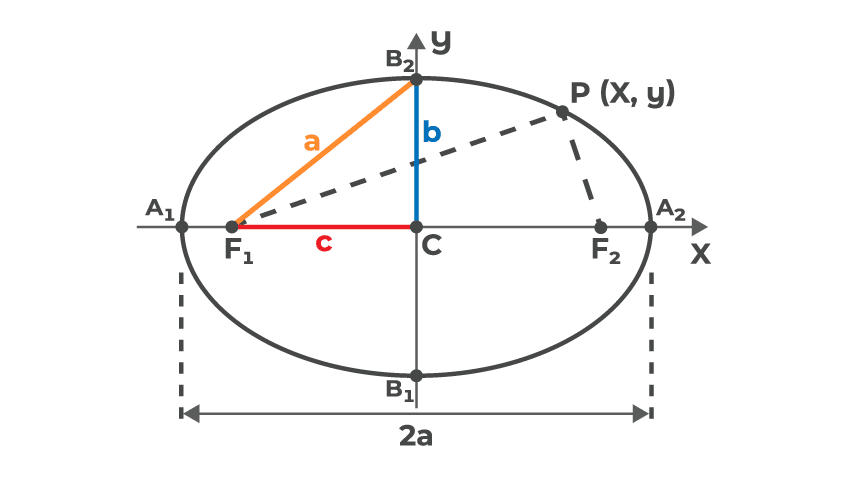
Os elementos da elipse apresentado na imagem são:

C → Centro da elipse;

F1 e F2 → Focos da elipse;

A1 e A2 → Extremidades do eixo horizontal da elipse;

B1 e B2 → Extremidades do eixo vertical da elipse;

c → é a distância entre um dos focos e o centro da elipse. 2 . c é a distância focal;

A distância que vai de A1 até C ou de A2 até C é chamada de semieixo maior (a);

A distância que vai de B1 até C ou de B2 até C é chamada de semieixo menor(b);

 

A elipse possui outra relação importante, a chamada excentricidade (e). Quanto maior for a excentricidade, mais achatada será a elipse e quanto menor for esse valor, mais próximo de uma circunferência a elipse irá se tornar. Podemos calcular a excentricidade fazendo a razão entre comprimento c e o semieixo maior:

 

e = c/a

Ficou com dúvidas? Deixe aqui seu comentário👇