Movimento harmônico simples

O movimento harmônico simples (MHS) ocorre quando um corpo oscila em torno de uma posição de equilíbrio.

 

Alguns exemplos de MHS estudados na física são:
- Oscilador massa-mola;
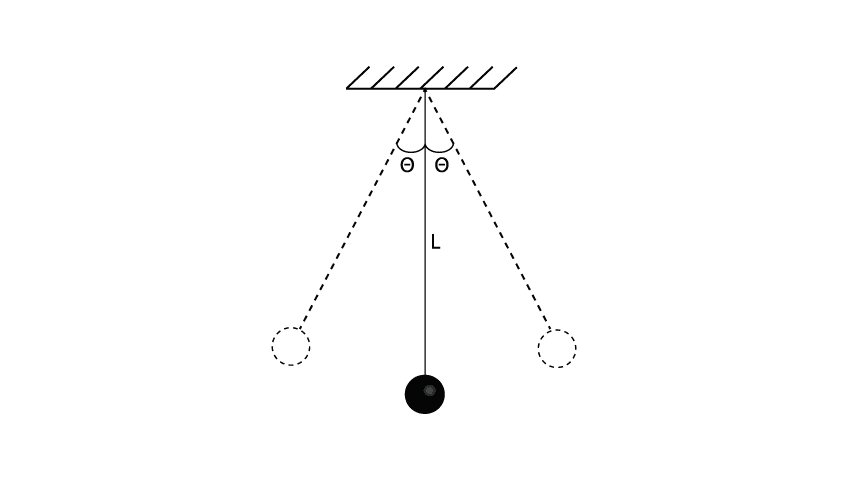
- Pêndulos (simples, torção, espirais, cônicos e outros).

 

No MHS a energia mecânica é constante, mas as energias cinética e potencial são opostas, ou seja; quando a energia potencial é máxima, a energia cinética é mínima e vice-versa.

 

As principais grandezas trabalhadas no MHS são:

 

- Frequência (f) – medida em hertz (hz, 1/s), a frequência mostra o número de oscilações por segundo realizadas por um sistema;

- Período (T) – medido em segundos (s), apresenta o tempo gasto em uma oscilação. O período é igual ao inverso da frequência: T = 1/f ;

- Frequência angular (ω) – medida em radianos por segundo (rad/s), mostra a velocidade de rotação do corpo em um sistema no MHS. Pode ser expressa por: ω = 2π/T, ou então, ω = 2πf;

- Amplitude (A) – media em (m), equivale à maior distância que um corpo chega com relação à sua posição de equilíbrio.

 

No estudo do MHS os osciladores mais cobrados em vestibulares e concursos são: pêndulo simples e oscilador massa-mola. Veja abaixo como ficam as equações da velocidade angular e o período, nestes dois casos.

 

- Pêndulo simples – ω = √g/L, T = 1/2 π . √L/g, com g sendo a gravidade e L o comprimento do pêndulo.

- Oscilador massa-mola – ω = √k/m, T =1/2 π. √m/k sendo k a constante elástica da mola e m a massa do bloco.

 

Por fim, as equações para a posição (X(t)), velocidade (v(t)) e a aceleração de um corpo em MHS, em um dado instante (t), e posição inicial (Θo), são:

 

X(t) = ω A cos(ωt+ Θo)
v(t) = - ω A sen(ωt+ Θo)
a(t) = - ω² A cos(ωt+ Θo)

 

Você gostou dessa dica de física? Deixe aqui seu comentário. 👇