Cinemática

A cinemática é a ciência que estuda a geometria do movimento, descrevendo-o por meio de três grandezas básicas: posição, velocidade e aceleração. Embora não esteja explícito nas grandezas estudas na cinemática, o tempo é fundamental para ela, pois as três grandezas citadas anteriormente são função dele. Neste wiki, abordaremos conceitos de trajetória e velocidade de um determinado corpo.

Ponto material x Corpo extenso

O ponto material nada mais é do que um corpo, ou partícula, que possui dimensões e estrutura interna insignificantes em relação às dimensões envolvidas no fenômeno descrito por este corpo. No entanto, quando as dimensões não podem ser descartadas, este corpo passa a ser chamado de corpo extenso.

Para que um corpo seja considerado um corpo extenso ou partícula, dependerá da escala do meio em que ele está se movimentando, por exemplo: para estudarmos o movimento de um carro em uma rodovia, não o tratamos como corpo extenso, mas sim como partícula, pois suas dimensões são desprezíveis em relação às dimensões da rodovia. Contudo, se estivermos estudando o movimento de um carro dentro de uma garagem, este passará a ser considerado um corpo extenso, já que suas dimensões são relevantes em relação às dimensões da garagem.

Referencial

Um referencial é um corpo ou lugar a partir do qual as observações de fenômenos provenientes de um ponto material são feitas. Assim, ao mudar o referencial, a percepção dos fenômenos também muda.

O referencial pode ser definido como o ponto de vista de um observador colocado em determinado lugar no espaço, por exemplo: em um jogo de baseball, quando a bola é rebatida, o torcedor na arquibancada e o juiz descrevem movimentos distintos da bola. Para estudarmos o movimento de um corpo com base em um referencial, este deverá ser arbitrário, para não interferir na trajetória do corpo. No exemplo citado acima, quaisquer referenciais, inclusive o juiz, não modificam o movimento da bola. Entretanto, para o estudo de um determinado movimento, o referencial deverá ser sempre o mesmo.

Posição

A localização de um corpo em relação a um referencial é indicada por meio de um sistema de  coordenadas, em geral cartesiano, com eixos x, y e z. Observe alguns exemplos:

Unidimensional

O movimento de um corpo para frente ou para trás em relação a um referencial, é determinado por um único eixo, o x, por exemplo, e a orientação deste corpo caracteriza uma geometria unidimensional. Se soltarmos um balão, por exemplo, na ausência de vento ou outros fatores externos, ele descreverá um movimento para cima somente. Arbitrando um eixo nessa direção (geralmente usa-se o eixo y para movimentos na vertical) e fazendo sua graduação (marcando pontos com distâncias predeterminadas), podemos determinar a posição da bola.

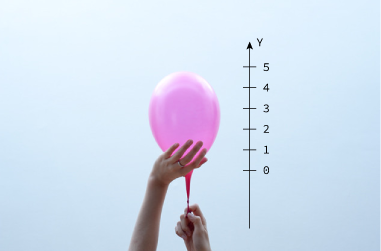
Bidimensional

Para o movimento de um carro sobre um cruzamento, sua localização é dada pelo uso de duas coordenadas (x e y). Sendo assim, o carro pode se movimentar para frente ou para trás, para esquerda ou para direita. Se usássemos apenas uma coordenada, isso limitaria a determinação da posição do carro. A orientação do carro sobre o cruzamento é caracterizada por uma geometria bidimensional.

Tridimensional

Já para o movimento de uma bola de futebol dentro de um estádio, sua localização é dada pelo uso de três coordenadas (x, y e z).  Por exemplo, poderíamos arbitrar os eixos x e y para descrever os movimentos da bola sobre o gramado (para frente e para trás; para a esquerda e para a direita) e, caso ela seja levantada, o movimento será descrito pelo eixo z, que irá representar a orientação do corpo (bola) para cima ou para baixo. A orientação da bola em um jogo de futebol é caracterizada por uma geometria tridimensional.

Repouso e movimento

Dependendo do referencial que adotarmos, um determinado corpo poderá estar em repouso e movimento ao mesmo tempo. Por exemplo, imaginemos que estamos indo de ônibus para a aula. Se nosso referencial for o motorista do ônibus, que está dentro do veículo em movimento, um indivíduo sentado dentro do ônibus não estará se movimentando em relação a esse referencial, mas estará em repouso. No entanto, se o referencial for alguém em um ponto de ônibus, esse mesmo indivíduo sentado dentro do ônibus agora estará em movimento, na mesma velocidade do veículo.

Como podemos observar as respostas dos referenciais são divergentes, porém ambas estão corretas, já que a definição de repouso e movimento é relativa.

Trajetória

Trajetória é o nome dado ao percurso realizado por um determinado corpo no espaço, com base em um sistema de coordenadas predefinido. Esse também é um conceito relativo, pois a posição de um corpo só pode ser definida quando se escolhe um referencial fixo. Um exemplo é a queda de um objeto em um trem em movimento com velocidade constante. Para o observador no trem, o objeto cairá em uma linha reta, mas para o observador do lado de fora do trem e parado, o objeto cairá e continuará se movendo com a velocidade do trem, o que seria visto como uma trajetória parabólica.

Espaço

Espaço é a posição de um corpo em relação a sua trajetória e, para determiná-la, um ponto O é escolhido de forma arbitrária como sendo a origem do movimento e uma orientação é dada à trajetória. Suponha que, durante uma viagem, o carro no qual você está, quebre na rodovia presidente Dutra, no km 100. Ao ligar para o guincho, você a utilizará como referência a fim de informar a sua localização, indicando a rodovia e o quilômetro em que está. Outro exemplo: Um carro sai do quilômetro 80 de uma rodovia e viaja até chegar em outra cidade, que se localiza no marco quilômetro 120. A variação de espaço nesta viagem corresponde a 40 km, pois o espaço inicial corresponde ao quilômetro 80 e o espaço final corresponde ao quilômetro 120, logo, a diferença entre eles equivale a 40 km. A escolha da origem e da orientação de uma trajetória não alteram a posição do carro.

Função horária do espaço

Quando observamos um objeto que se movimenta, notamos que a sua posição se altera com o passar do tempo. Sendo assim, temos uma fórmula que relaciona matematicamente os espaços (S) desse objeto com os instantes correspondentes (t) e chamamos isso de função horária do espaço. No caso particular de a velocidade de um corpo ser constante, ou seja, não variar, a fórmula da função horária do espaço é: , como veremos posteriormente ainda neste artigo. Nessa fórmula, “S” representa o espaço final, “S₀” o espaço inicial, “v” é a velocidade do corpo e “t” o tempo decorrido no trajeto entre “S” e “S₀”.

Exemplo:

Um caminhão, de 30 m de comprimento tem velocidade constante de 20 m/s. Calcular o tempo gasto para passar uma ponte de 60 m de comprimento.

Temos que a distância total após a passagem total do caminhão foi 30 m (comprimento do caminhão) + 70 m (comprimento da ponte) = 100 m. E, como a velocidade é constante, sabemos que a fórmula da função horária do espaço é:

Dessa maneira:

s = 100; s₀ = 0; v = 20 m/s; t = ?

Então:

100 = 0 + 20.t

100 = 20t

100 / 20 = t

t = 5 s.

O caminhão leva 5 s para atravessar a ponte.

Exemplo:

Dada a função horária do espaço, , com t em segundos e s em metros, qual será o espaço do corpo nos instantes t=2, t=3, t=4 e t=5?

                 
                 
                 
                 

Variação do espaço x distância percorrida

Indicamos pela letra grega delta () a variação de uma grandeza, ou seja, a diferença entre os valores dessa grandeza entre um instante inicial e um instante final.

Assim, para a variação de espaço: se um objeto, em um momento , possui posição e, em um momento , possui posição _, temos que  é a variação de tempo e  é a variação de espaço.

Em relação à definição de variação do espaço, podemos afirmar: se é maior do que , logo será maior do que zero e, sendo assim, o corpo se move no sentido positivo da trajetória. Contudo, se for menor do que , o será menor do que zero e, sendo assim, o corpo se move no sentindo negativo da trajetória. Se for igual a , o será igual a zero e, desta forma, o objeto não se move ao longo da trajetória.

A distância percorrida é a grandeza que indica o quanto uma partícula se moveu entre dois instantes e sempre é dada em valor absoluto (positivo).

Exemplo:

Um corpo vai de = 8 km até = 100 km e depois retorna a = 50 km:

a :

= 100 km – 8 km = 92 km

a :

= 50 km – 100 km = – 50 km

Perceba que de a a variação do espaço é positiva, mas de a é negativa, porque há a inversão do movimento (o corpo retorna), e a variação do espaço final da partícula pode ser calculada simplesmente pela diferença entre seu espaço final e  inicial:

a :

 = 50 km – 8 km = 42 km

A distância percorrida, entretanto, é a soma dos módulos (valores absolutos) de cada uma dessas variações e, ao final do trajeto, terá um valor diferente da variação do espaço:

a : Percorreu 92 km para ir

a : Percorreu 50 km ao voltar

Então, de a o total que o corpo percorreu foi 142 km, ainda que a variação do espaço tenha sido de apenas 42 km:

d = |92 |+ |-50| = 92 + 50 = 142 km.

Velocidade escalar média

A velocidade escalar média é definida como a razão entre o espaço percorrido por um móvel e o tempo total gasto para percorrer tal espaço. A equação a seguir define essa grandeza:

Exemplo:

Se um automóvel em uma viagem percorrer 100 km em 2 horas, podemos concluir que o carro percorreu, em média, 50 km a cada hora.

 = 100 km
 = 2h

Repare que não significa que o carro se movimentou somente nesta velocidade. Ele pode ter variado a velocidade durante todo o trajeto. O valor que calculamos é a velocidade média () do carro, que é definida como sendo a razão entre a variação de espaço (), e a variação de tempo ().

Velocidade escalar instantânea

A velocidade escalar instantânea é o limite da velocidade escalar média, quando o intervalo de tempo tende a zero:

É ela que está indicada no velocímetro do carro, por exemplo: a velocidade do corpo naquele exato instante.  Assim, para sabermos a velocidade de um objeto a todo instante, a velocidade escalar média não tem utilidade, precisamos, na verdade, da velocidade escalar instantânea.

Movimento progressivo e movimento retrógrado

Se um móvel se desloca no mesmo sentido da orientação da trajetória, o valor do espaço aumenta com o passar do tempo e, com isso, seu deslocamento escalar é positivo. Nesse caso, o movimento é classificado como progressivo e a velocidade é positiva (v > 0).

Por outro lado, se o móvel se desloca no sentido contrário ao da orientação da trajetória, o valor do espaço diminui com o passar do tempo e, com isso, seu deslocamento é negativo. Nesse caso, o movimento é classificado como retrógrado e a velocidade é negativa (v < 0).

Movimento uniforme (MU)

Chamamos de movimento uniforme um movimento em que, em instantes de tempo iguais, percorre-se espaços de mesmos tamanhos, uma vez que não há variação da velocidade. Em outras palavras: no movimento uniforme, a velocidade escalar instantânea se mantém constante e diferente de zero.

Para que um movimento seja considerado uniforme, ele não necessariamente precisa ser realizado em uma reta, apenas manter a velocidade constante. Mas, se ele, de fato, acontecer em uma trajetória retilínea, iremos chamá-lo de movimento retilíneo uniforme (MRU), como o movimento de um carro em uma estrada sem trânsito, no limite de velocidade permitido. Por outro lado, o movimento pode acontecer em uma trajetória circular, como o de um satélite em uma órbita circular ao redor da Terra. Nesse caso, o movimento será um movimento circular uniforme (MCU).

Função horária no MU

No movimento uniforme, a velocidade média da partícula, a todo instante, coincide com a velocidade instantânea, uma vez que não há variação desta última. Então, temos:

Se o corpo começa seu movimento em um espaço s₀, em um tempo t₀, e o termina em um espaço s, em um tempo t, então podemos escrever:

Se considerarmos que o movimento se inicia no tempo t₀=0, chegamos na função horária do MU (a célebre equação do “sorvete”):

Por meio da equação acima, conseguimos determinar o espaço em que um corpo, com uma determinada velocidade constante, estará depois de um certo tempo.

Exemplo:

Um corpo que se move em um MU possui função horária s = 20 + 10t, sendo o espaço dado em metros e o tempo em segundos. Depois de 10s, qual será seu espaço? Em que instante ele estará no espaço s = 100 m?

Para saber onde o corpo estará após 10s, basta substituir t = 10 na função horária:

s = 20 + 10.10 = 20 + 10

s = 30 m

Para saber quanto tempo o corpo leva para chegar ao espaço 100 m,

substituímos s = 100 na função horária:

100 = 20 + 10t

100 – 20 = 10t

t = 80/10

t = 8 s