Dilatação térmica

A dilação térmica é um assunto muito estudado devido a sua importância e aplicação, como por exemplo em projetos de engenharia de estruturas e em ferrovias.

Dilatação dos sólidos

A maioria dos corpos está sujeita a variações de temperatura que causam variações nas suas dimensões, ou seja, os corpos se dilatam termicamente. A dilatação térmica é estudada principalmente em corpos sólidos, devido à facilidade de observação da dilatação ou contração do corpo.

Como a temperatura se relaciona com a distância entre as partículas de um corpo, podemos concluir que um aumento da temperatura causa dilatação enquanto uma diminuição da temperatura causa contração do material.

De maneira a simplificar os estudos, consideraremos apenas os corpos isótropos, que são aqueles que possuem as mesmas propriedades físicas em quaisquer direções.

A dilatação pode ser unidimensional, ocorrendo apenas em uma única dimensão, bidimensional, quando ocorre em uma área (duas dimensões) ou tridimensional, quando as dimensões do volume variam.

Dilatação linear

Após várias experiências o homem percebeu que se um corpo com um comprimento inicial L_i e temperatura inicial T_i for submetido a um aumento de temperatura, ele vai sofrer um alongamento, ou seja, a variação da temperatura ΔT causa uma variação no comprimento ΔL do corpo, conforme figura abaixo.

Neste caso (linear) a área transversal deve ser desconsiderada.

Outro fator que influencia na dilatação do corpo e está relacionado ao material é o coeficiente de dilatação linear (α). A tabela abaixo apresenta o valor de α para alguns materiais.

Esse coeficiente na verdade dita a relação de proporcionalidade entre as variáveis ΔL (variação de comprimento), L_i (comprimento inicial) e ΔT (variação de temperatura), conforme equação abaixo:

Isolando ΔL, obtemos a equação usual para a dilatação linear dos sólidos:

Dilatação superficial

Assim como na dilação linear, quando temos uma área S_i submetida a uma variação de temperatura ΔT o corpo sofrerá uma variação na área ΔS. No caso da área também existe um fator que contribui com a sua variação, e este é conhecido como coeficiente de dilatação superficial (β). A figura abaixo ilustra o processo de dilatação superficial.

De forma análoga ao que fizemos para a dilatação linear, podemos chegar em duas equações, uma que descreve a variação da área ΔS e outra que descreve a área final S_f no processo de dilatação superficial:

Relação entre α e β

Analisando os coeficientes da dilatação linear em relação ao coeficiente da dilação superficial (duas dimensões) podemos concluir que

Dilatação volumétrica

Assim como visto nos tópicos acima, um volume inicial V_i submetido a uma variação de temperatura ΔT sofrerá uma variação no volume ΔV. Aqui o fator que contribui com a dilatação é o coeficiente de dilatação volumétrica (γ). A figura a seguir exemplifica a dilatação volumétrica.

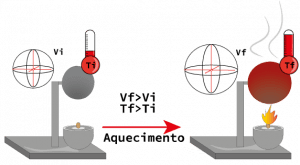
As equações que apresentam a variação de volume ΔV e o volume final V_f são descritas a seguir.

Relação entre α e γ

Fazendo analogia com a relação entre alfa e beta, aqui podemos concluir que o coeficiente gama (três dimensões) vale três vezes o valor de alfa, ou seja,

Dilatação em corpos vazados ou com furos

Todos os corpos vazados ou com furo quando submetidos a variação de temperatura ΔT se comportam como corpos maciços. No exemplo apresentado na figura abaixo, conforme a temperatura aumenta o raio do furo também aumenta.

Variação da densidade

Sabemos que a densidade de um corpo é a razão entre a sua massa e o seu volume (). Como a massa de um corpo não varia com a alteração da temperatura, mas o volume sim, podemos usar a fórmula da dilatação volumétrica para encontrar uma relação entre a densidade final do corpo d_f e a variação da temperatura ΔT sofrida por ele, conforme equação abaixo:

Nessa equação é importante destacar que quanto maior for a temperatura menor será a densidade.

Dilatação real e aparente nos líquidos

Considerando que os líquidos assumem a forma do recipiente que ocupam, devemos nos atentar ao fato de que o recipiente também pode sofrer deformação.

Analisando a figura acima, podemos observar que quando o frasco é aquecido (II) ele aumenta seu volume, logo o nível aparente do líquido diminui. Em (III), o líquido entra em equilíbrio com o frasco fazendo com que suas temperaturas fiquem iguais e ambos sofrem dilatação. Após o entendimento da imagem, podemos resumir:

1. De I para II consideramos apenas a dilatação do recipiente, sem a dilatação do líquido;
2. De II para III, com o recipiente já dilatado, consideramos agora só a dilatação do líquido.
3. De I para III então, temos a dilatação aparente do líquido, onde consideramos a dilatação do recipiente junto com a do líquido.

Para a dilatação em líquidos temos então dois coeficientes: de dilatação real e de dilatação aparente. O primeiro está relacionado com o líquido e é absoluto enquanto o segundo coeficiente depende do recipiente, logo é relativo.

A partir dos coeficientes de dilatação do líquido e das conclusões sobre a figura acima, podemos concluir que:

No caso de um recipiente ideal, para o qual a dilatação é desprezível, podemos simplificar a expressão:

Comportamento anômalo da água

Normalmente os líquidos se dilatam quando submetidos a um aumento de temperatura. Um líquido muito utilizado no dia-a-dia, á água, apresenta um comportamento um pouco diferente. Na faixa entre 0 e 4º C ela apresenta uma contração, e somente após essa temperatura começa a sofrer dilatação. A figura abaixo apresenta um gráfico do comportamento da água.

Consequentemente, outra propriedade da água que apresenta um comportamento anômalo é a densidade. Na figura abaixo podemos observar que na faixa entre 0 e 4º C, a densidade aumenta e somente após 4º C diminui.

O comportamento anômalo da água pode ser observado quando colocamos um recipiente com água no congelador da geladeira e forma-se uma superfície com gelo enquanto a água submersa está no estado líquido. Isso acontece porque a 4°C a água tem densidade máxima e por isso fica abaixo do gelo, que já está a 0°C (com densidade menor).