Prismas

O que você precisa estudar hoje?

Voltar
Você está aqui:
porEquipe Realize Educação

Na geometria espacial, dentre diversos sólidos estudados, o prisma se destaca muito pela sua utilidade cotidiana. Além disso, os prismas englobam uma vasta quantidade de representantes distintos, mas que compartilham de importantes características em comum, características que estudaremos a seguir.

Definição de prisma

O prisma é um poliedro da geometria euclidiana formado por dois polígonos congruentes contidos em dois planos paralelos, de forma que cada vértice de um dos polígonos se ligue ao vértice correspondente do outro através de uma aresta, formando um sólido geométrico de características muito peculiares.

Desenho de um prisma octogonal.
Exemplo de um prisma.

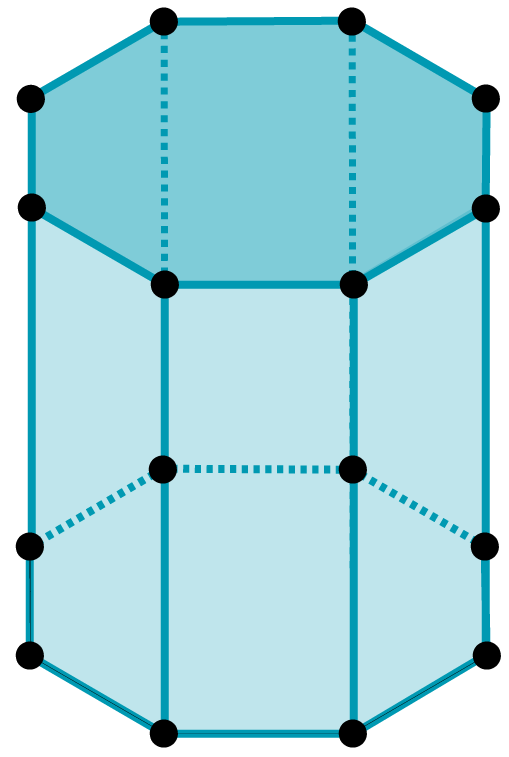
Elementos de um prisma

Todo prisma possui duas faces chamadas de bases, uma inferior e outra superior, formadas por dois polígonos congruentes; arestas laterais, que conectam os vértices dos polígonos da base superior ao seu correspondente na base inferior e, portanto, estão presentes em mesmo número que os vértices desses polígonos; arestas das bases, que definem os lados dos polígonos das bases do prisma; uma altura, que liga os planos de cada uma das bases do sólidos, perpendicularmente a estes. Além disso, por se tratar de um sólido, cada prisma possui uma medida de volume, e medidas de superfície lateral (área lateral) e superfície total (área total), como podemos ver na figura abaixo.

Desenho de um prisma com detalhamento de seus elementos (faces, arestas, altura).
Elementos de um prisma.

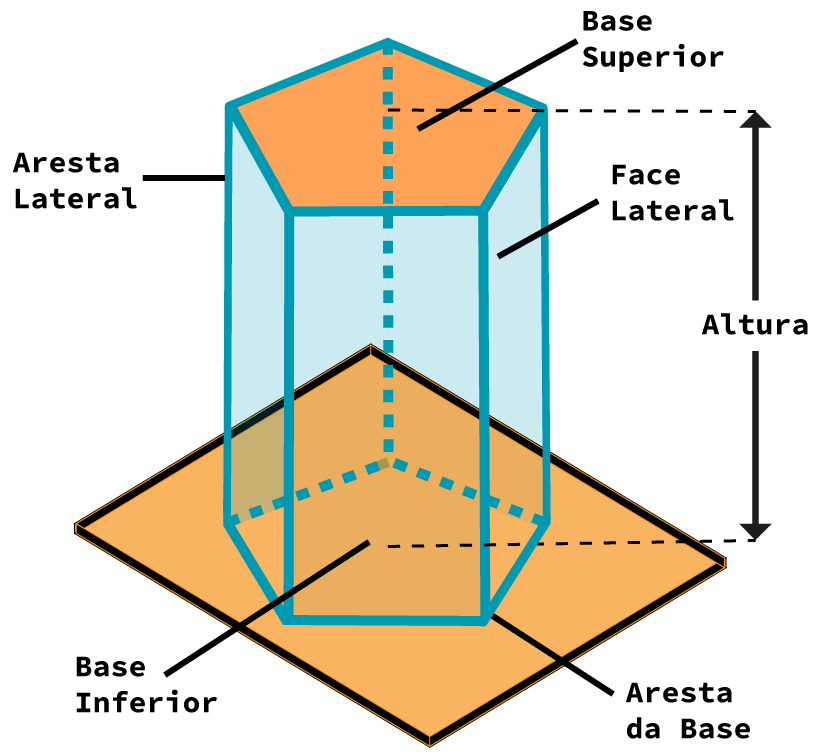
Classificação dos prismas

Podemos classificar prismas como oblíquos, quando suas arestas laterais são oblíquas às bases, ou seja, não são perpendiculares em relação às bases:

Desenho de um prisma oblíquo pentagonal.
Exemplo de um prisma oblíquo.

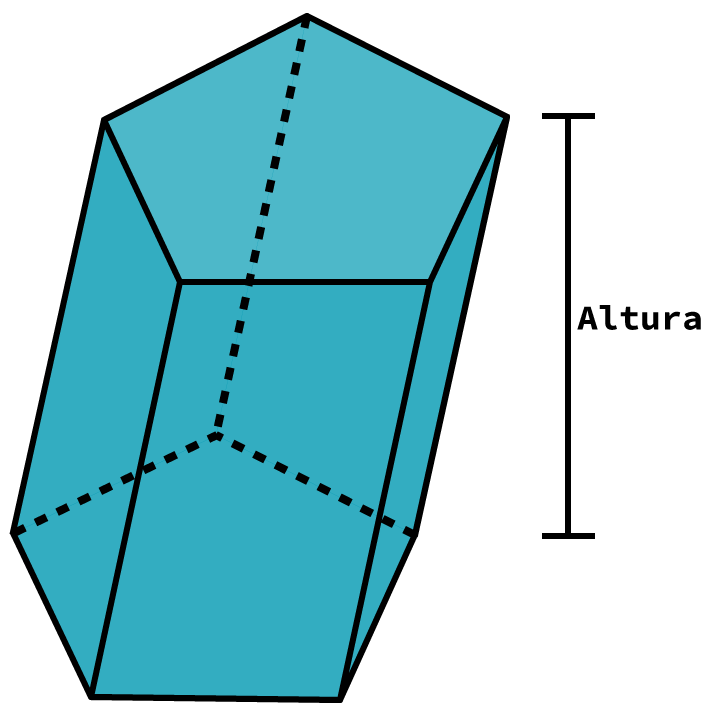
Como prismas retos, aqueles que possuem arestas laterais perpendiculares às bases, sendo o prisma regular um caso específico do prisma reto no qual as bases são polígonos regulares.

Desenho de um prisma reto pentagonal.
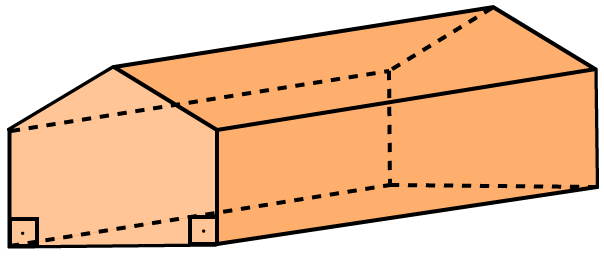
Exemplo de um prisma reto qualquer.
Desenho de um prisma reto pentagonal
Exemplo de um prisma reto regular.

Natureza dos prismas

Os exemplos de prismas possíveis tende ao infinito, uma vez que a natureza de um prisma depende, somente, da quantidade de lados dos polígonos das bases. E, assim, alguns polígonos notáveis são muito utilizados para diversas áreas do estudo.

Alguns exemplos de prismas são:

Prisma triangular

Os prismas triangulares são aqueles cujas bases são triângulos.

Desenho de um prisma triangular.
Exemplo de um prisma triangular.

Prisma quadrangular

Os prismas quadrangulares são aqueles cujas bases são quadriláteros.

Desenho de um prisma quadrangular.
Exemplo de um prisma quadrangular.

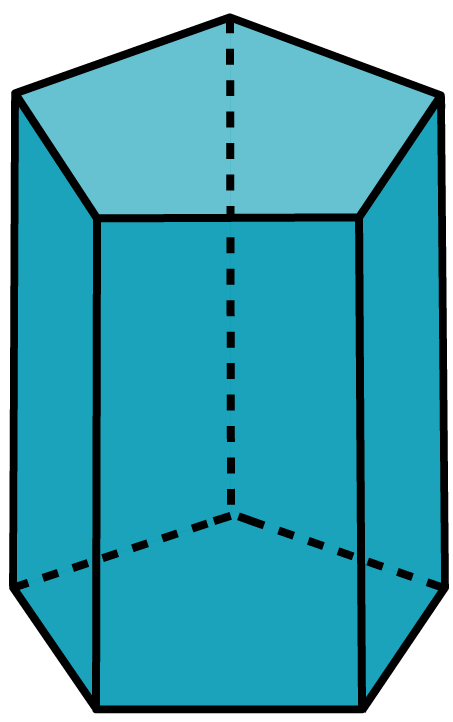
Prisma pentagonal

Os prismas pentagonais são aqueles que possuem bases pentagonais.

Desenho de um prisma pentagonal.
Exemplo de um prisma pentagonal.

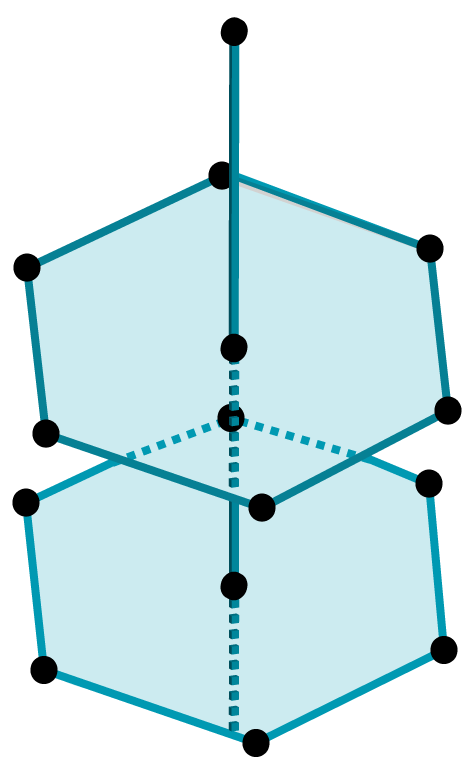
Prisma hexagonal

Os prismas hexagonais são aqueles que possuem bases em forma de hexágono.

Desenho de um prisma hexagonal.
Exemplo de um prisma hexagonal.

Área da base

Para diversos cálculos que envolvem o prisma, saber calcular a área da base é muito importante. Assim, por se tratar de diversas bases distintas, para inúmeras possibilidades de prismas, vejamos abaixo algumas bases notáveis de prismas regulares e o cálculo de suas áreas:

Base triangular

A base triangular de um prisma regular é um triângulo equilátero e, assim como na geometria euclidiana plana, calculamos sua área pela fórmula S_{b} = \frac{l \times h}{2}, na qual S_{b} representa a área da base triangular do prisma, l o tamanho do lado da base do triângulo e h a altura do triângulo.

Desenho de um triângulo equilátero com indicação de seus vértice e tamanho do lado.
Base do prisma triangular – triângulo equilátero.

Contudo, pelo teorema de Pitágoras temos que:

l^{2} = h^{2} + \left(\frac{l}{2}\right)^{2}, assim h = \frac{l \cdot \sqrt{3}}{2}.

Portanto, a área da base do prisma retangular pode ser dada pela fórmula S_{b} = \frac{l \cdot \sqrt{3}}{4}

Base quadrada

Quando um prisma reto possui bases quadradas, a área de cada uma de suas bases pode ser dada pela área do quadrado, de modo que S_{b} = l^{2}.

Desenho de um quadrado com indicação do tamanho do lado.
Base do prisma quadrado.

Base hexagonal

Quando um prisma reto possui bases hexagonais, a área de cada uma de suas bases pode ser dada pela área do hexágono regular.

Inscrevendo um hexágono regular em uma circunferência podemos observar que o diâmetro dessa circunferência pode ser delimitado por dois vértices do hexágono, dividindo-o em duas metades.

Desenho de um hexágono inscrito em uma circunferência.
Hexágono regular inscrito em uma circunferência.

Assim, repetindo a mesma marcação com os demais vértices, são gerados seis triângulos equiláteros com lados medindo o raio da circunferência.

– Desenho de um hexágono divido em seis triângulos equiláteros, inscrito em uma circunferência.
Hexágono dividido em seis triângulos equiláteros.

Dessa maneira, chamando cada lado dos triângulos equiláteros de “l“, temos a área de cada um dos triângulos dada por S_{tri} = \frac{l \cdot h}{2} e pelo teorema de Pitágoras h = \frac{l \cdot \sqrt{3}}{2}.

Desenho de um hexágono divido em seis triângulos equiláteros, inscrito em uma circunferência. Indicação da altura e lado do triângulo equilátero.
Determinação da altura do triângulo equilátero.

Com isso, a área do triângulo equilátero é dada por S_{tri} = \frac{l^{2} \cdot \sqrt{3}}{4} e, consequentemente, a área do hexágono será seis vezes a área do triângulo equilátero, ou seja, S_{hex} = \frac{3 l^{2} \cdot \sqrt{3}}{2}.

Apótema da base

Considerando um prisma regular e uma base qualquer desse prisma inscrita em uma circunferência, definimos apótema dessa base como o segmento de reta “a” que vai do centro da circunferência dada até o ponto médio de um dos lados do polígono.

Desenho de um octógono com Indicação do seu apótema.

Apótema “a” de uma base poligonal.Alguns apótemas são notáveis, como o apótema de uma base quadrada que é dado por a = \frac{l}{2} e, também, o apótema da base hexagonal, dado por a = \frac{l \cdot \sqrt{3}}{2}

Área lateral

A área lateral de um prisma compreende toda a superfície do sólido, retirando suas bases poligonais, ou seja, a área lateral de um prisma qualquer pode ser dada pela fórmula S_{L} = n \cdot l \cdot H, em que H é a altura do prisma, l é o tamanho do lado do polígono da base e n o número de vértices do polígono da base.

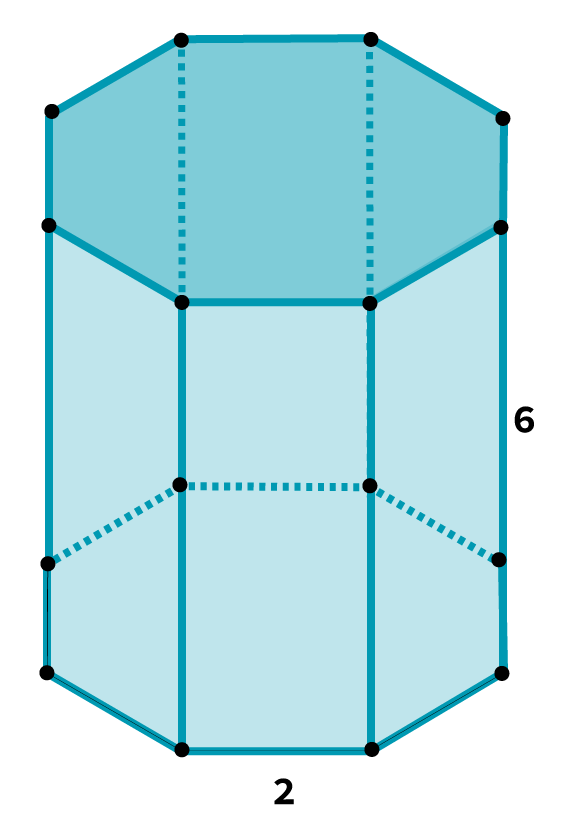
Exemplo:

A área lateral de um prisma de base octogonal de lado l = 2 , altura H = 6  é dada por S_{L} = 8\times 2\times 6 = 96 unidades de área.

Desenho de um prisma octogonal com Indicação do comprimento e altura de suas faces.
Prisma de base de lado 2 e altura de medida 6.

Área total

A área total de um prisma é dada pela adição da área lateral com as áreas das duas bases poligonais, cobrindo toda superfície do sólido, sendo a superfície de um sólido dada por toda região plana que o sólido pode cobrir.

Desenho de um cubo com sua planificação.
Prisma quadrangular e sua planificação.

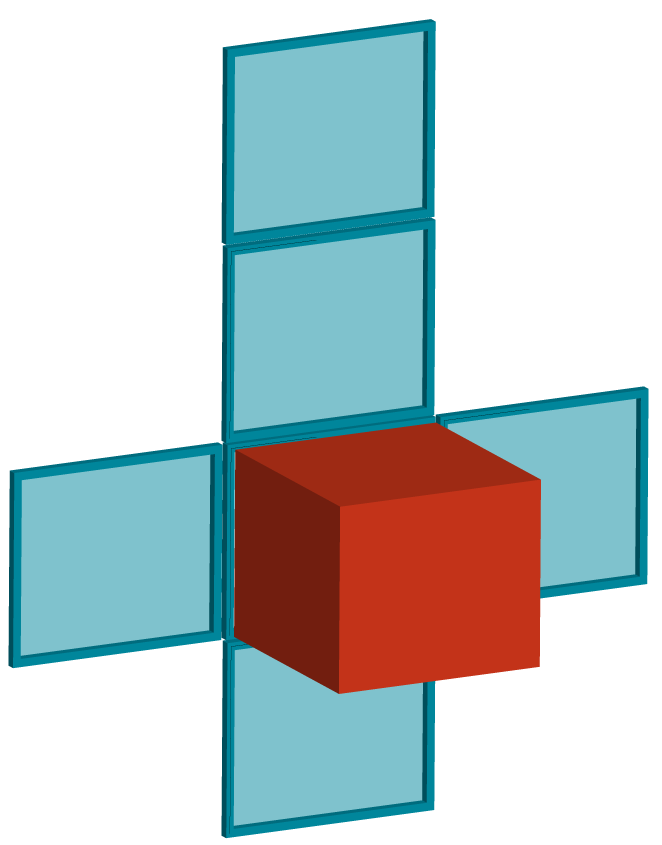
Senso assim, a área total de um prisma qualquer pode ser dada por S_{t} = 2 \cdot S_{base} + S_{L}.

Exemplo:

Dado um prisma quadrangular regular de lado da base l = 2 e altura H = 3, calcular sua área total.

S_{base} = l^{2} = 2^{2} = 4

S_{L} = n \cdot l \cdot H = 4 \times 2 \times 3 = 24

S_{t} = 2 \cdot S_{base} + S_{L} = 2 \times 4 + 24 = 32 unidades de área

Volume do prisma

O volume de um prisma é dado pela medida espacial de seu interior, ou seja, trata-se da capacidade do sólido em questão em uma unidade de medida tridimensional.

Para se pensar em volume de prismas, considere uma base poligonal de determinada área S_{B} . Podemos sobrepor n bases idênticas consecutivas de forma que cubram determinado espaço, centradas em um segmento de reta H  perpendicular aos planos que contém as bases consecutivas. Assim, conseguimos sobrepor as superfícies da base H vezes, de forma que  o volume do prisma será V_{P} = S_{B} \cdot H. O volume do prisma é dado pelo produto entre a área de sua base e sua altura.

Desenho de duas bases hexagonais dispostas uma sobre a outra.
Superfícies congruentes dispostas em um eixo central.

Prismas notáveis

Alguns prismas são tão usuais na matemática e no dia-a-dia que acabam possuindo um estudo mais aprofundado de suas fórmula e definições, além de possuírem nomes exclusivos.

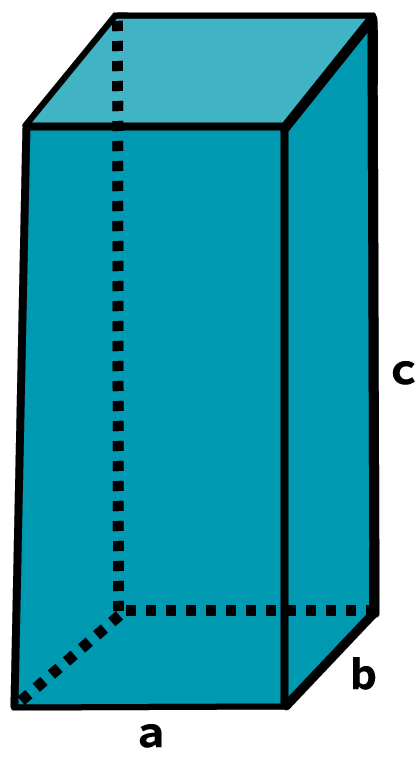
Paralelepípedo retângulo reto

O paralelepípedo retângulo reto é um prisma de base retangular de lados l_{1} e l_{2} e uma altura H.

A área lateral desse prisma pode ser dada pela fórmula S = 4 \cdot l_{1} \cdot H, uma vez que todo retângulo possui quatro lados delimitando, consequentemente, quatro faces para o prisma.

A área total do paralelepípedo, assim como em qualquer prisma, é dada pela soma das áreas da base com a área lateral, resultando em S_{t} = 2 \cdot l_{1} \cdot l_{2} + 4 \cdot l_{1} \cdot H, ou ainda, S_{t} = 2 \cdot l_{1} (l_{2} + 2H ).

O volume, por sua vez, pode ser dado por V = l_{1} \cdot l_{2} \cdot H, uma vez que a área de todo retângulo é dada por S_{ret} = l_{1} \cdot l_{2}.

Além dos conceitos acima, podemos definir a diagonal do paralelepípedo. Sendo a diagonal de um sólido todo segmento de reta dado pela ligação de dois vértices não consecutivos, podemos calcular a diagonal do paralelepípedo pela fórmula D^{2} = l_{1}^{2} + l_{2}^{2} + H^{2}, uma vez que a diagonal d da face da base é dada por \sqrt{l_{1}^{2} + l_{2}^{2} }.

Desenho de um paralelepípedo com indicação de seu comprimento, altura, largura e diagonal.
Paralelepípedo reto e suas características.

Triângulo laranja \Rightarrow d^{2} = a^{2} + b^{2} (1)

Triângulo vermelho \Rightarrow D^{2} = c^{2} + d^{2} (2)

Substituindo (2) em (1):

D^{2} = a^{2} + b^{2} + c^{2}

Cubo

Outro prisma notável é o cubo, cujas bases são quadradas de lado l e a altura desse prisma também mede l.

Dessa forma definimos a área lateral do cubo como S_{L} = 4 \cdot l^{2}, uma vez que a base possui quatro vértices, além da área total S_{t} = 6 \cdot l^{2}.

Além disso, o volume do cubo, dado pela multiplicação da área da base pela altura, pode ser dado como V = l^{3}.

E, análogo ao paralelepípedo anterior, a diagonal do cubo pode ser dada por D^{2} = l^{2} + l^{2} + l^{2}, assim D^{2} = 3 \cdot l^{2}.

Desenho de um cubo com indicação de seu comprimento, altura, largura e diagonal.
Cubo e suas características.
Tags:

Deixe um comentário